The Zero of the function is the value of the algebraic function where the function is equal to zero or unresolvable. For algebraic polynomials, there can be some values where the process equals zero. We actually equate a function to zero to solve the values of the equation.
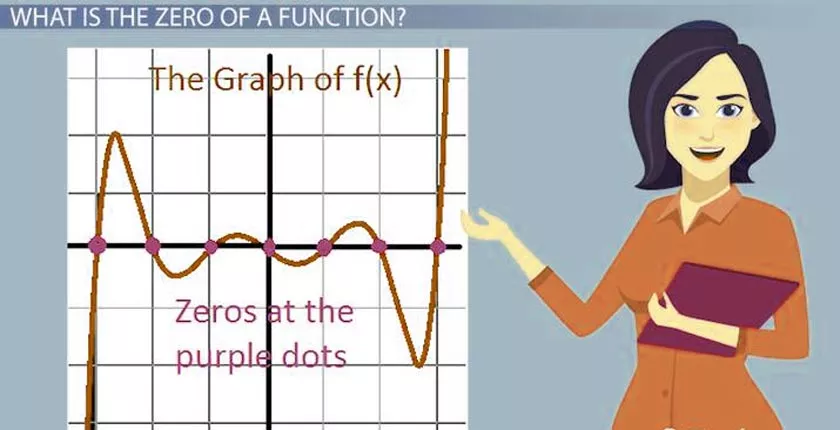
Zeros of a Function And Roots of the Algebraic Equation?
Use the Zeros Calculator to find the zeroth values of the function. The values are known to be the Zeroth value of a polynomial. The polynomial function calculator makes it simple to find the Zeroth values of the polynomial.
You need to compare a function with zero, when finding the roots of an algebraic function like 5×2+8x+3=0, 5×2+9x+4=0, and 12×2+15x+3=0, etc. The polynomial function needs to solve to find the values of th variable.
Zero of Quadratic Equation:
The Zeroth equation is used to find the roots of the function, consider the following functions. Here we find the roots of the quadratic functions by comparing them with the Zero.
- 5×2+9x+4=0——————–(1)
- 5×2+8x+3=0————–(2)
- 12×2+15x+3=0——————–(3)
the roots of the quadratic equation are:
5×2+9x+4=0——————–(1)
x=-4/5, x=-1
5×2+8x+3=0————–(2)
x=-3/5 , x=-1
12×2+15x+3=0——————–(3)
12x+3=0 , x+1=0
The complex finding zeros calculator by calculator-online.net is used to find the root of the quadratic equation having real roots.
Solution of Equation 1:
Now consider the equation:
5×2+9x+4=0——————–(1)
5×2+5x+4x+4=0
5x(x+1)+4(x+1)=0
(5x+4)(x+1)=0
(5x+4)=0 and (x+1)=0
5x+4=0 , x+1=0
x=-4/5 , x=-1
The roots of 5×2+9x+4=0 are x=-the 4/5 , x=-1 of the quadratic equation. You can only find the roots of this algebraic function by comparing it with the zero.
Solution of Equation 2:
Take the equation 2:
5×2+8x+3=0————–(2)
5×2+5x+3x+3=0
5x(x+1)+3(x+1)=0
(5x+3)(x+1)=0
(5x+3)=0 and (x+1)=0
5x+3=0 , x+1=0
x=-3/5 , x=-1
The roots of 5×2+8x+3=0- are x=-3/5 , x=-1 of the quadratic equation. find the roots of this algebraic function by comparing it with the zero.
Solution of Equation 3:
Take quadratic equation # 3, here you can solve it by the factorization method.
You can write the equation as
12×2+15x+3=0——————–(3)
12×2+12x+3x+3=0
12x(x+1)+3(x+1)=0
(12x+3)(x+1)=0
(12x+3)=0 and (x+1)=0
12x+3=0 , x+1=0
x=-3/12 , x=-1
x=-1/4 , x=-1
Roots are x=-the 1/4 , x=-1 of the quadratic equation. use the complex zero calculator for the complex numbers.
Conclusion:
The Zeros theorem is commonly used to find the roots of the functions. It is the point that no solution to the quadratic equation is possible and we are comparing the algebric equation with the zero to find its roots.
The Zeros Calculator is a simple way to find the real or the complex roots of the equation. It is essential to compare an equation with zero to find its roots.
